In signal processing, filtering is an essential process, which removes unwanted components from the signal. A special class of filters is finite impulse response (FIR) filters, which we will discuss in more detail in this paper. After a brief description of digital filters, we will discuss the structure and function of FIR filters. We summarize the implementation of FIR filter in measurement software OXYGEN.
What is a digital filter?
A digital filter is a mathematical algorithm that processes signals to extract information and remove unwanted information, such as blocking or passing through a certain frequency range. Therefore, it is a digital system that converts the input sequence into the output sequence through the conversion process.
There are different types of filters. However, according to the length of the impulse response, we can divide digital filters into the following categories:
Infinite impulse response (IIR)
Finite impulse response (FIR)
Unlike analog filters implemented with electronic components (such as capacitors, coils, resistors, etc.), digital filters are implemented with logic devices (such as ASIC, FPGA) or in the form of sequential programs of signal processors.
What is the difference between IIR and FIR filters?
In general, IIR and FIR filters have different responses to input pulses. If the impulse response of the filter drops to zero after a finite time, it is called a FIR filter (finite impulse response). On the other hand, if the impulse response is infinite in time, it is an IIR filter (Infinite impulse response). Whether or not the impulse response of a digital filter drops to zero after a finite time depends on how the output value is calculated. For FIR filters, the output value depends only on the current and previous input values, while for IIR filters, the output value also depends on the previous output value.
Compared with FIR filter, IIR filter has the advantage that performing similar filtering operations usually requires fewer coefficients, faster operation speed and less memory. However, a big disadvantage of IIR filters is their nonlinear phase response. For applications that do not require phase information, such as monitoring signal amplitude, IIR filters are very suitable. However, for applications requiring linear phase response, FIR filters are generally more suitable.
How does the FIR filter work?
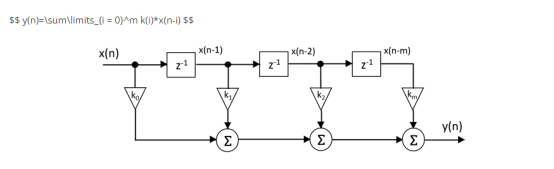
Figure 1 shows the functional operation of FIR filter. At the input, the data/value x (n) is applied clock by clock (sample by sample) of the A/D converter.
In the above line, there is a shift element (z-1), which shifts the data/value applied to the input one step for each clock cycle. This means that at the end of the following example, the value x (n-3) is 3 clock cycles earlier than the current value x (n). In the middle is the FIR coefficient k0 - km. These coefficients represent an amplifier that multiplies the input value by the gain k. The next line is the summation branch, which adds all the results of multiplication (integration). The output y (n) is the processed signal obtained from the FIR coefficient, which can be expressed by the following mathematical expression:
In OXYGEN software FIR filter
OXYGEN is our intuitive test and measurement software. It is an integrated software for measurement, visualization and various application analysis. Therefore, it includes various features, including FIR filter. It is an easy to use tool, allowing you to choose from four different filter types:
Low pass
high pass
Bandpass
Band stop
Once selected, just input the filter length, the required window function, and whether to compensate the signal delay, and you can start. For more detailed instructions on how to set FIR filter in OXYGEN, please contact the authorized dealer Beiying Electronics.
In short
A digital filter is a mathematical algorithm that processes signals to extract and/or delete unwanted information. FIR filter is a kind of filter with finite impulse response length, because it tends to zero in a finite time. Compared with IIR filter, FIR filter is fundamentally more stable and can be designed as linear phase.



